i² = -1, и это проблема. Физики сто лет спорят, нужны ли «мнимые» числа для описания реальности (кажется, ответ найден)

Сто лет назад странное поведение атомов и элементарных частиц заставило физиков придумать новую теорию природы. Так родилась квантовая механика. Она сразу показала свою силу - с ее помощью удалось очень точно описать, как атом водорода излучает и поглощает свет. Но в самой формуле теории с самого начала сидела проблема. В центральном уравнении квантовой механики неожиданно появлялось мнимое число i, квадрат которого равен -1.

Физики прекрасно понимали, что i - чистый математический трюк. Реальные физические величины вроде массы или импульса при возведении в квадрат никогда не дают отрицательного значения. Тем не менее именно это "нереальное" число с свойством i² = -1 оказалось в самом сердце квантового мира. После того как Эрвин Шредингер вывел свое знаменитое уравнение, напичканное мнимыми числами, он честно признался, что надеется заменить его полностью "настоящей", то есть вещественной версией. В 1926 году он писал, что в нынешнем виде в уравнении "безусловно есть некоторая грубость". Но сколько бы Шредингер ни ворчал, i в теории так и осталось, а новые поколения физиков просто привыкли к его уравнению и перестали переживать.

Интерес к этой странности вспыхнул заново в 2021 году. Группа исследователей предложила экспериментальную схему, которая должна была ответить на принципиальный вопрос - является ли i действительно необходимой частью квантовой теории или это лишь удобный математический костыль. Две независимые команды довольно быстро поставили очень тонкие эксперименты и заявили, что получили однозначное подтверждение: квантовая механика действительно нуждается в мнимых числах. Однако в этом году серия новых работ перевернула этот вывод.

Весной теоретики из Германии показали, что можно построить квантовую теорию, в которой все значения - только вещественные числа, и при этом она полностью эквивалентна стандартной, комплексной версии. Затем двое физиков из Франции предложили свою собственную реализацию "вещественной" квантовой механики. А в сентябре другой исследователь, рассматривая задачу уже с точки зрения квантовых вычислений, пришел к тому же выводу: чтобы описывать квантовую реальность, i на самом деле не обязательно. При этом новые формулировки избегают явного использования мнимых чисел, но сохраняют характерные следы их арифметики. Из-за этого часть специалистов сомневается, удалось ли действительно выгнать "мнимость" из квантовой теории и из описания реальности.

Чтобы понять, откуда вообще взялись такие числа, приходится вернуться в XVII век. В 1637 году Рене Декарт, живший тогда в Амстердаме на пике тюльпанной лихорадки, сталкивался с уравнениями, решения которых казались невозможными. Разбирая пример x³ - 6x² + 13x - 10 = 0, он писал, что корни "бывают не всегда реальны, но иногда только мнимы, и не всегда есть величина, которой соответствует то, что воображают". Корнями этого уравнения являются числа 2, 2 - i и 2 + i. Последние два имеют реальную и мнимую часть и записываются как a + ib. Такие числа позже назвали комплексными. Декарт относился к ним с презрением, но со временем комплексные числа стали незаменимым инструментом в геометрии, оптике, теории сигналов и во многих других областях.

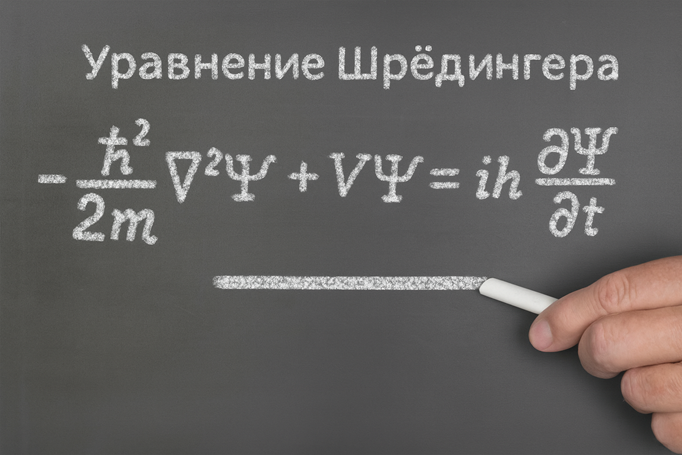
Шредингеру тоже не нравилась их "нереальность", но он был вынужден признать, что с ними квантовые расчеты сильно упрощаются. Его уравнение описывает эволюцию волновой функции - объекта, который задает все возможные квантовые состояния системы и позволяет объяснить, как эти состояния складываются и гасят друг друга наподобие волн. Волновая функция у Шредингера изначально комплексная, хотя все реальные измерения дают только вещественные значения. Многие физики обращали внимание, что квантовая теория стала первой физической теорией, где комплексные числа оказались прямо в центре формализма.

Математически комплексное число можно представить как точку на плоскости, где по горизонтали откладывается реальная часть a, а по вертикали - мнимая часть b. Каждое комплексное число превращается в вектор из начала координат в точку с координатами (a, b). Эти векторы живут по особым правилам. Например, умножение на i поворачивает вектор на 90 градусов. Именно такие свойства очень удобно описывают квантовые состояния, которые тоже ведут себя как векторы с необычными правилами сложения и поворотов. Некоторые физики пытались отказаться от комплексных чисел и переписать все только на вещественном языке. В 1960 году швейцарский физик Эрнст Штюкельберг предложил "вещественную" квантовую механику, которая с помощью математических хитростей заставляла реальные числа имитировать повороты вокруг "мнимой" оси. Однако там, где стандартная теория выглядела компактной, вещественная версия получалась очень громоздкой.

Тем не менее позже было показано, что даже такая реальная версия способна воспроизводить ключевые эффекты квантовой теории, например результаты знаменитых тестов Белла, связанных с квантовой запутанностью. Но оставался вопрос - всегда ли "вещественная" теория даст те же предсказания, что и комплексная. В 2021 году группа исследователей во главе с Николя Жизеном решила усложнить тест Белла, чтобы проверить пределы реальных чисел. Вместо классической схемы с двумя участниками и одной парой запутанных частиц они рассмотрели эксперимент с двумя независимыми источниками запутанных фотонов и тремя наблюдателями. Расчеты показали, что для теории, построенной только на вещественных числах, существует предел максимальной корреляции измерений, а для комплексной квантовой теории этот предел выше. Появилось впечатление, что теперь можно экспериментально отличить одну версию от другой.

Скоро группа в китайском университете науки и технологий в Хэфэе реализовала этот протокол и показала, что реальные измеренные корреляции значительно превышают предел для вещественной теории. На первый взгляд это выглядело как приговор: без комплексных чисел квантовую механику не построить. Однако теоретики, выступившие с критикой в этом году, внимательно разобрали математическую основу работы 2021 года и указали на ключевое предположение. Авторы исходной статьи просто перенесли в вещественную теорию стандартную операцию тензорного произведения, которая используется для объединения состояний нескольких квантовых систем в одно. Немецкая и французская группы утверждают, что это неверный шаг: для теории, целиком построенной на вещественных числах, правило комбинирования векторов должно быть более общим. Они предложили другую, более широкую схему "склейки" состояний, в рамках которой можно построить вещественную квантовую теорию, дающую ровно те же предсказания, что и обычная комплексная.

Независимая линия аргумента пришла из квантовых вычислений. Квантовые компьютеры управляют состояниями кубитов с помощью так называемых логических вентилей. Один из ключевых элементов, вентиль T, вращает вектор состояния кубита на комплексной плоскости. В сентябре исследователь из Google Quantum AI Крейг Гидни показал, что любой квантовый алгоритм можно переписать таким образом, чтобы полностью избавиться от вентилей T. Фактически это стало численным доказательством того, что для квантовых вычислений можно обойтись без явного использования комплексных чисел.

Все это приводит к неудобному, но интересному выводу. Формально квантовая теория действительно не обязана опираться на i. Ее можно переложить на язык вещественных чисел, хотя получится заметно сложнее и тяжеловеснее. При этом в этих "очищенных" версиях все равно сохраняются следы прежней арифметики - правила комбинирования величин устроены так, будто за кулисами по-прежнему работают комплексные числа. Некоторые исследователи говорят в лоб, что на самом деле мы просто симулируем комплексные числа с помощью вещественных.

Философы физики и сами физики спорят, как это понимать. Одни считают, что комплексная квантовая механика с ее естественным тензорным произведением и наглядной геометрией векторов остается более красивой и удобной формой. Другие надеются, что отказ от i поможет сформулировать теорию заново, на более простых и интуитивных принципах. Пока же никакой по-настоящему новой, альтернативной версии квантовой механики за сто лет так и не появилось, и главный вопрос звучит все так же остро: почему наша фундаментальная теория работает именно так и можно ли когда-нибудь выйти за пределы привычной формулы, с которой все началось.