Корень из минус единицы правил квантами 100 лет. Теперь ученые исполнили мечту Шрёдингера и выкинули i… но что-то пошло не так

Ровно сто лет назад странности поведения атомов заставили физиков создать новый язык природы — квантовую механику. Она сразу проявила силу, позволив точно рассчитать спектр водорода, но в её уравнениях неизбежно возникла мнимая единица i (корень из −1). Величины вроде массы и импульса при возведении в квадрат не дают отрицательных значений, а здесь появилась величина, для которой i² = −1. Эрвин Шрёдингер, записав уравнение движения, надеялся впоследствии заменить комплексную запись полностью вещественной, однако этого так и не произошло: физики приняли необходимость комплексной формы. В 2021 году к теме вернулись — предложили проверить, действительно ли i принципиально необходимо. Две исследовательские группы поставили тонкие эксперименты и заявили, что без мнимых компонентов не обойтись. В 2025-м сразу несколько статей оспорили этот вывод.

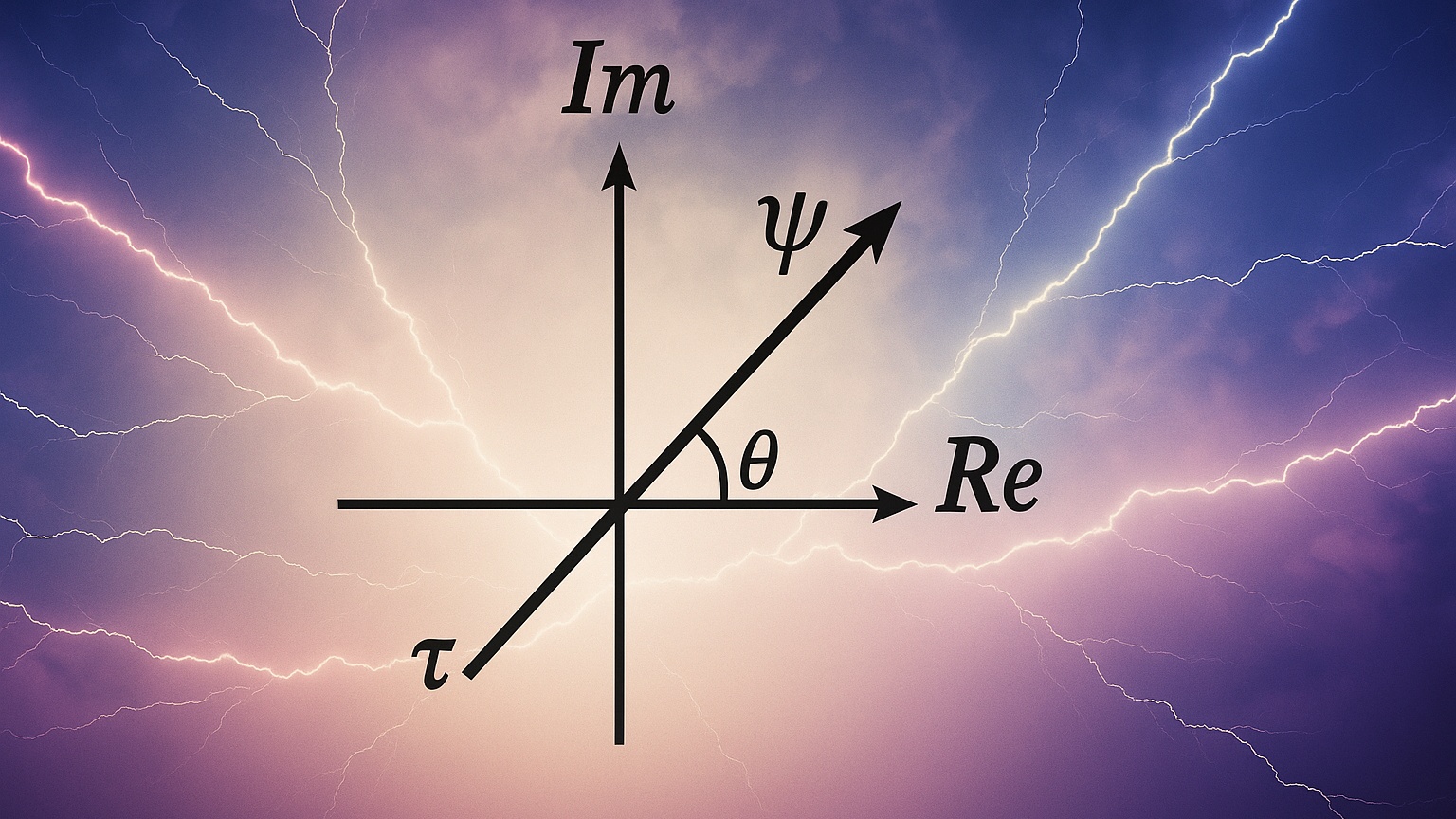
Суть спора — в том, как представлять квантовые состояния. Волновая функция в стандартной формулировке имеет комплексные значения; математически это вектор на комплексной плоскости Аргана, где действительная часть располагается на оси x, а мнимая — на оси y, а умножение на i соответствует повороту вектора на 90 градусов. Такая геометрия естественно описывает интерференцию и фазовые сдвиги. При этом приборы всегда измеряют реальные числа. Возникает соблазн построить эквивалентную теорию, использующую только действительные величины — без явного присутствия i, но с сохранением всех наблюдаемых эффектов.

Попытки такого перехода предпринимались давно. В 1960 году Эрнст Штюкельберг показал, как перенести динамику из комплексного гильбертова пространства в вещественное: «повороты» по мнимому направлению можно имитировать специальными преобразованиями. Цена за это — громоздкость описания: система из двух частиц, вместо четырёх комплексных амплитуд, требует шестнадцати вещественных. Тем не менее в 2008–2009 годах независимые группы продемонстрировали, что «реальная» версия способна воспроизводить результаты тестов Белла — стандартной проверки квантовой нелокальности. Однако оставалось открытым, можно ли добиться полного совпадения с обычной теорией во всех ситуациях.

В 2021 году опубликованная работа привлекла особое внимание. Её авторы предложили усовершенствованный протокол с двумя независимыми источниками запутанных частиц и тремя участниками (Алиса, Боб, Чарли). Математический анализ показал различие верхних границ корреляций для двух типов теорий: при вещественной записи существует один предел согласованности измерений, а при комплексной — более высокий. Проведённый затем эксперимент в Хэфэе действительно дал результаты, превысившие «реальную» границу, что интерпретировали как подтверждение незаменимости i.

В 2025 году теоретики из Германии указали на скрытое допущение в этом рассуждении: при объединении подсистем использовалось стандартное тензорное произведение, естественное для комплексного гильбертова пространства. Для полностью вещественной теории это правило не обязано сохраняться. Как теорема Пифагора точно описывает плоское пространство, но изменяется на сфере, так и способ объединения пространств состояний может быть иным. Переписав композицию более общим образом, исследователи построили целиком вещественную механику, дающую те же статистические предсказания, что и комплексная. Вслед за ними двое физиков во Франции независимо предложили эквивалентную формулировку с иной, но согласованной операцией объединения подсистем. А осенью работа из области квантовых вычислений добавила ещё один аргумент: анализируя набор логических вентилей, автор показал, что от фазового «T-вентиля» (геометрически — поворот состояния на комплексной плоскости) можно отказаться без потери вычислительной мощности. Вывод прозрачен: даже квантовая логика не требует обязательного присутствия мнимых чисел.

Следует, однако, помнить: полностью вещественные формулы неизбежно воспроизводят операции, аналогичные умножению на i — те же повороты и фазовые сдвиги, только выраженные через удвоенный набор действительных координат и более сложную алгебру. Именно поэтому стандартная комплексная запись остаётся короче и нагляднее: в ней тензорные произведения, фазовые множители, интерференция и динамика Шрёдингера складываются в единый, компактный язык.

С философской точки зрения вопрос звучит так: если i можно «спрятать» во внутренние вычисления и оперировать только действительными величинами, отражает ли это реальное свойство природы или лишь удобство выбранного описания? Одни видят в новых работах аргумент в пользу того, что мнимая единица — инструмент, а не элемент физической реальности. Другие напоминают: даже в «реальном» варианте сохраняются черты комплексной арифметики — вращения, фазы и интерференционные соотношения, естественнее всего выражающиеся именно на комплексной плоскости. Возможно, разгадка кроется в самих квантовых свойствах, таких как спин, которые не имеют классических аналогов и органично описываются через комплексные амплитуды.

На данный момент вывод двойственный. Эксперименты 2021–2022 годов, утверждавшие, что «без i нельзя», опирались на конкретный выбор тензорной структуры, не уникальной для вещественных построений. Альтернативные правила объединения снимают это ограничение и дают совпадение всех предсказаний. Значит, вещественные формулировки возможны и физически эквивалентны стандартной записи. При этом классическая комплексная форма остаётся короче и удобнее для расчётов. Спор теперь смещается с вопроса «нужно ли i» к более глубокому: почему именно комплексный язык оказывается настолько естественным для описания квантового мира, тогда как чисто вещественный требует многословных эквивалентов. Ответа, который бы радикально пересмотрел механику, у нас пока нет.