1 кубик — на краю. 100 — над бездной. Эта башня не упадёт даже если повиснет над Гранд-Каньоном

Представьте простой эксперимент , который легко провести прямо у себя дома . Возьмите детские кубики или блоки от Дженги и положите один на самый край стола. Начинайте сдвигать его вперёд, пока он почти не упадёт — так, чтобы ровно половина блока свисала в воздухе. Удивительно, но он не рухнет: пока центр тяжести находится над поверхностью стола, конструкция остаётся устойчивой. Стоит выдвинуть чуть дальше — и гравитация возьмёт своё.

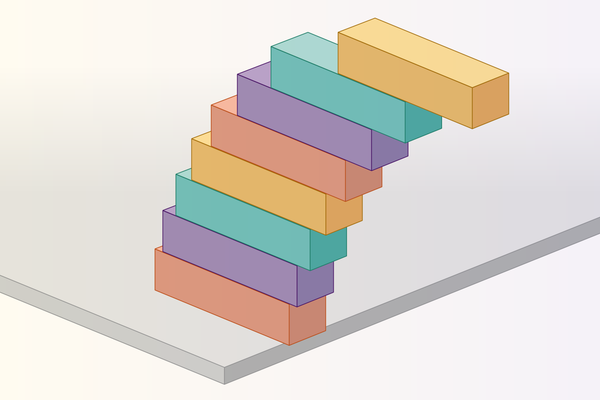
Теперь поставьте сверху второй блок. Сколько теперь получится сдвинуть верхний элемент за край, прежде чем всё разрушится? А если добавить третий? Четвёртый? С каждым уровнем эксперимент становится всё интереснее.

Интуиция подсказывает, что конструкция не может выдаваться за край дальше длины одного блока. Но математика отвечает иначе: теоретически башню можно вытянуть на любую дистанцию — хоть через весь стол, хоть за край каньона. Без клея и магии, всё держится исключительно за счёт распределения масс и одного бесконечного ряда.

Центр масс — это точка, в которой условно сосредоточена вся масса объекта. Для симметричного кубика он расположен строго посередине. Пока центр тяжести остаётся над опорой — конструкция сохраняет равновесие. Выходит за пределы — наступает обрушение. Именно поэтому один кубик можно безопасно выдвинуть наполовину своей длины: в этом случае центр масс окажется как раз на границе стола.

С добавлением второго блока ситуация усложняется: теперь важно учитывать положение общего центра тяжести всей конструкции. Верхний блок по-прежнему выдвигается на ½ длины относительно нижнего, но теперь уже сам нижний можно сдвинуть только на ¼ — чтобы общий центр тяжести всей двухблочной системы оставался строго над опорой. Почему именно четверть? Потому что центр тяжести верхнего находится на ¼ длины вправо от края, а нижнего — на ¼ влево. В сумме получается идеальный баланс.

Добавляя третий, четвёртый, пятый блок — вы получаете закономерность: верхний выдвигается на ½, следующий — на ¼, далее 1⁄6, 1⁄8, 1⁄10, 1⁄12… Эти доли уменьшаются, но не исчезают. Каждый новый блок добавляет немного к общему выносу конструкции.

Чтобы разобраться в механике, представьте: у вас уже есть устойчивая башня из пяти блоков, и вы хотите добавить шестой снизу. В этом случае можно считать верхнюю часть одной массой, условно равной 5. Нижний блок — масса 1. Центр масс верхней части смещается над краем нижнего, а он сам — выдвигается вперёд на 1⁄12. Это тот самый принцип рычага: чтобы уравновесить пять единиц массы сверху, одну внизу нужно разместить в пять раз дальше от центра.

В итоге формируется математическая формула: общий вынос — это сумма ряда 1⁄2 + 1⁄4 + 1⁄6 + 1⁄8 + 1⁄10 + …, то есть половина знаменитого гармонического ряда: 1 + 1⁄2 + 1⁄3 + 1⁄4 + … Этот ряд бесконечен: слагаемые становятся всё меньше, но сумма продолжает расти — пусть и очень медленно. К примеру, сумма первых 100 000 членов — всего около 12,1. А миллион даст примерно 14,4. Но рост есть — а значит, предела нет.

Разумеется, в реальности вы не соберёте башню длиной в десятки метров. Воздух, трение, неточности в форме блоков, микроколебания и давление на нижние уровни своё дело сделают. Но на уровне цифр ограничений нет. В вашем распоряжении бесконечность — если бы были идеальные условия и бесконечный запас терпения.

Хотите попробовать сами? Уже четырёх блоков или карт хватит, чтобы верхний элемент можно было выдвинуть за край почти полностью: суммарный вынос составит чуть больше одной длины блока — ½ + ¼ + 1⁄6 + 1⁄8 ≈ 1.04. А чтобы получить выступ в две длины, потребуется 31 блок. На десять — уже около 100 миллионов. Гармонический ряд растёт медленно, но неумолимо.

Этот простой эксперимент — на самом деле наглядный математический урок . Он показывает, как из обычных объектов можно извлечь глубокие закономерности. Даже повседневные предметы подчиняются строгим физическим законам , которые открывают путь к неожиданным открытиям. И это напоминание: сложная наука нередко прячется в самых простых играх.

Тем более, что современные инструменты позволяют не только проводить подобные опыты вживую, но и моделировать их на компьютере.