Сложить банан с яблоком не получится. А вот 3 + 11 = 2 — легко, если вы в группе
Помните, как в школе вы ненавидели алгебру? Зря — она умеет решать Кубики Рубика.

Вы перемешали Кубик Рубика и теперь хотите вернуть его в исходное состояние. Какую последовательность ходов нужно выполнить? Неожиданно, на этот вопрос можно ответить с помощью современной алгебры.
Большинство людей, прошедших школьный курс математики, наверняка посещали уроки алгебры — возможно, даже две ступени «Алгебра I» и «Алгебра II», где приходилось находить x. Слово «алгебра» обычно вызывает в памяти громоздкие многочлены вроде ax² + bx + c = 0 или графики функций y = ax² + bx + c.
Скорее всего, вы также помните квадратичную формулу, которая помогает найти решения таких уравнений и точки пересечения графика с осью x.
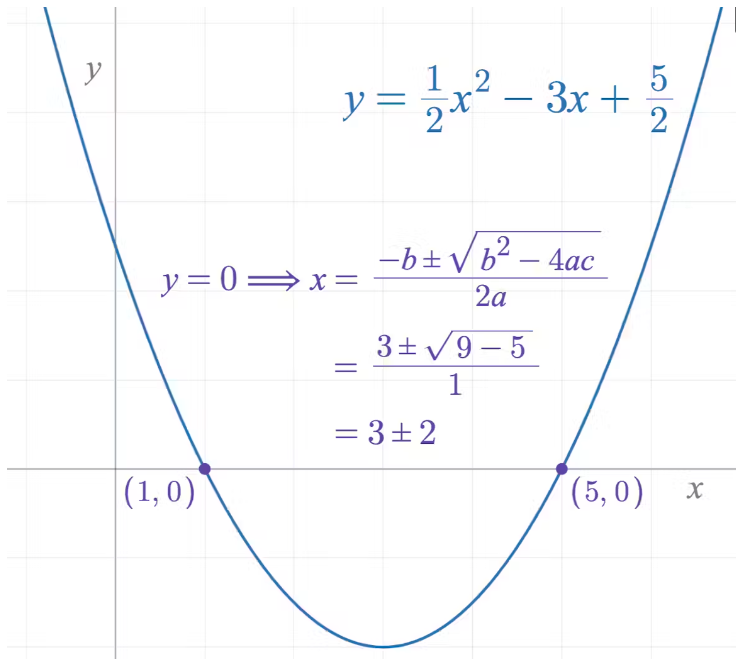
График квадратичного уравнения и его корней, полученных через квадратную формулу. Jacob Rus, CC BY-SA
Такие уравнения и графики — лишь часть алгебры. Главное в ней — изучать объекты — например, повороты Кубика Рубика или числа на циферблате — и то, как они ведут себя, когда их комбинируют. Что произойдёт, если последовательно выполнять кубические ходы или складывать часы?
Как показывают исследования математиков, многие алгебраические задачи сводятся к классификации объектов по сходству их поведения.
Как же от уравнений вида ax² + bx + c = 0 математики пришли к абстрактной алгебре?
Короткий ответ таков: формулы, похожие на квадратичную, нашли для полиномов третьей и четвёртой степеней, но не для пятой. Лишь Эварист Галуа с помощью разработанной им теории групп доказал, что единой формулы для полиномов пятой и более высоких степеней не существует.
Так что же такое группа? Начнём с множества — набора объектов. Чаша с фруктами на кухне — это множество, элементы которого — яблоки и бананы. Числа от 1 до 12 тоже образуют множество. Пока мы просто держим их вместе, свойств немного, но как только начинаем что-то делать с фруктами или числами, становится интереснее.
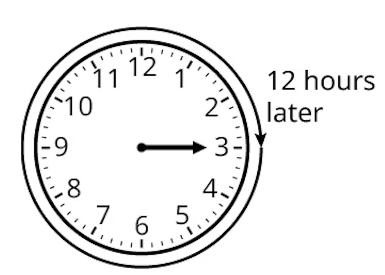
В часовой арифметике 3 + 12 = 3. OpenStax, CC BY-SA
Назовём числа от 1 до 12 «часовыми». Тогда можно определить сложение по правилам времени: например, 3 + 11 = 2, ведь через 11 часов после трёх будет два.
Часовое сложение имеет ряд приятных свойств. Оно замкнуто: сумма любых двух часовых чисел снова даёт часовое число. У него есть нейтральный элемент — 12, прибавление которого ничего не меняет. Операция ассоциативна, поэтому скобки можно расставлять как угодно. Для каждого числа существует обратное, отменяющее его действие. И, наконец, сложение коммутативно: a + b = b + a.
Благодаря этим свойствам часы с часовым сложением образуют группу. А вот бананы с яблоками из фруктовой чаши в группу не собрать — что получится, если «сложить» банан с яблоком? Зато числам на циферблате достаточно показать, что их сложение подчиняется указанным правилам, — и группа готова.
Помимо групп, введение в современную алгебру знакомит ещё с двумя базовыми объектами — кольцами и полями. Если добавить к часовому сложению вторую операцию — часовое умножение, при котором 2 × 7 = 2, потому что 14 часов соответствует двум, — то вместе они удовлетворяют распределительному закону a(b + c) = ab + ac. В этом случае часовые числа образуют кольцо. А поле — это кольцо, в котором выполняются ещё более строгие условия.
В начале XX века математики Давид Гильберт и Эмми Нётер, исследуя математические основы теории относительности Эйнштейна, объединили эти идеи и показали, насколько полезно изучать именно группы, кольца и поля.
Группы, кольца и поля звучат абстрактно, но применяются повсюду. Например, симметрию молекул классифицируют при помощи точечных групп, описывающих такие перемещения, после которых молекула остаётся неотличимой от исходной.
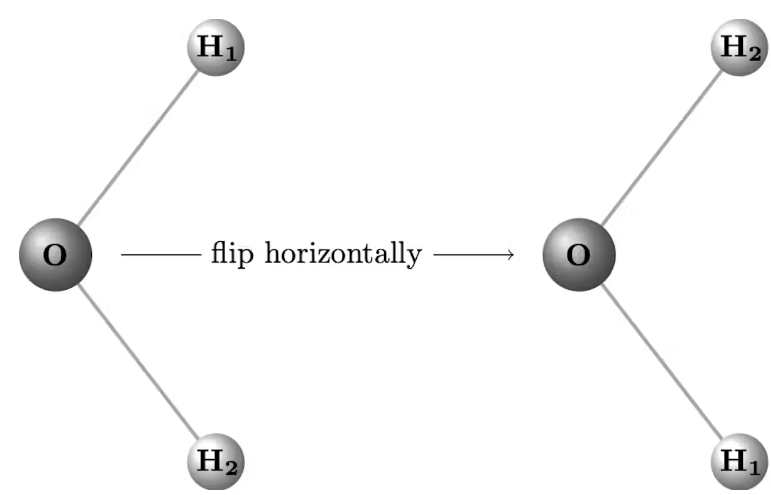
Молекулу воды H₂O можно отразить горизонтально, и мы получим конфигурацию, неотличимую от исходной. Courtney Gibbons, CC BY-SA
Возьмём пример для колец. Задачу описать судоку можно свести к системе уравнений: нужны 81 переменная для каждой клетки, полиномиальные выражения, кодирующие правила, и выражения, учитывающие исходные подсказки.
Чтобы связать клетку и переменную, используют двойной индекс: x₃₅ обозначает клетку в третьей строке и пятом столбце.
Каждая клетка может содержать только цифры 1–9, что записывается так: (x₁₁ − 1)(x₁₁ − 2)…(x₁₁ − 9) = 0. Равенство выполнится тогда и только тогда, когда подставлено допустимое число, и уже это даёт 81 уравнение.
Условие «в первой строке каждая цифра встречается ровно один раз» формулируется так: сумма строки x₁₁ + x₁₂ + … + x₁₉ − 45 = 0, а произведение x₁₁ x₁₂ … x₁₉ − 9·8·7·6·5·4·3·2·1 = 0.
Если кажется, что на составление этих уравнений уходит больше времени, чем на решение судоку вручную, вы правы.

Преобразование судоку в алгебраическую задачу требует немало усилий.
Зачем же все эти преобразования? Они позволяют использовать алгоритмы конца XX века, описывающие структуру особого кольца — идеала, заданного правилами и подсказками. Алгоритмы мгновенно сообщат, бывает ли у головоломки ноль решений, а если решений несколько — найдут их все.
Это лишь небольшой пример, где подготовка алгебры сложнее самой задачи. Но приёмы легко масштабируются: те же трюки, что помогают решить судоку или Кубик Рубика, применимы к задачам искусственного интеллекта, робототехники, криптографии, квантовых вычислений и не только.

