Тайна 126-го измерения раскрыта. Только теперь всё стало ещё запутаннее

Наш мозг привык оперировать представлениями о трехмерном пространстве. Логично предположить, что добавление очередной координаты просто расширяет возможности для движения, сохраняя базовые свойства - бескрайность и равномерность. Однако математическая реальность преподнесла исследователям удивительные сюрпризы в последнее время.

В мирах высших размерностей каждое пространство проявляет собственный уникальный характер. Восьмое и двадцать четвертое измерения позволяют расположить сферические тела с небывалой компактностью - такая плотность недостижима ни в одной другой системе координат. Некоторые геометрические структуры содержат "экзотические" сферы, напоминающие безнадежно смятые поверхности. А математические узлы, знакомые нам по реальным веревкам, существуют только в привычном трехмерном мире - в любом пространстве выше третьего ранга их можно распутать, даже не освобождая концы.

Современным ученым удалось завершить масштабное исследование, длившееся более шести десятилетий. Математическое сообщество стремилось выяснить, какие системы координат допускают существование настолько сложно организованных фигур, что их невозможно преобразовать в сферу даже с помощью специальной методики под названием "surgery" (дословно - хирургическая операция). Наличие подобных конструкций, как показали расчеты, неразрывно связано с фундаментальными топологическими вопросами о природе взаимоотношений между сферическими телами различных порядков.

Многолетние изыскания позволили установить, что такие искривленные объекты возникают в пространствах 2-го, 6-го, 14-го, 30-го и 62-го рангов. Более того, исследователи доказали принципиальную невозможность их появления во всех остальных координатных системах - за исключением одной. Статус 126-мерного пространства оставался загадкой.

В конце прошлого года международная группа специалистов наконец поставила точку в этой истории. В опубликованной работе Вейнань Линь и Гочжэнь Ван из Фуданьского университета совместно с Чжоули Сюй из Калифорнийского университета в Лос-Анджелесе математически утверждают: система 126-го порядка действительно входит в элитный список пространств, где возможно формирование этих удивительных геометрических структур.

От догадок к открытию

Научное сообщество пережило настоящее потрясение в 1950-х, когда Джон Милнор обнаружил в семимерном пространстве удивительный феномен . Он выявил существование "экзотических" сфер - объектов, которые с позиций топологии (науки, изучающей свойства фигур при деформации) неотличимы от классических аналогов. Однако эти структуры обладали принципиально разными характеристиками гладкости: линия, плавная на обычной поверхности, могла оказаться изломанной на экзотической. Количество таких необычных форм варьировалось от нескольких единиц до тысяч в зависимости от рассматриваемого измерения.

Для исследования загадочных конструкций Милнор как раз создал революционный метод преобразования математических многообразий. Этот подход стал фундаментальным инструментом в изучении геометрических структур высших порядков.

Математическая "операция", как и медицинская, подразумевает иссечение участка фигуры с последующим внедрением новых элементов по контуру разреза. Ключевое требование - сохранение безупречной гладкости в местах соединения, без образования острых граней или вершин. При работе со сложными структурами специалисты учитывают также их "фреймирование" - специальную характеристику, описывающую расположение объекта в пространстве.

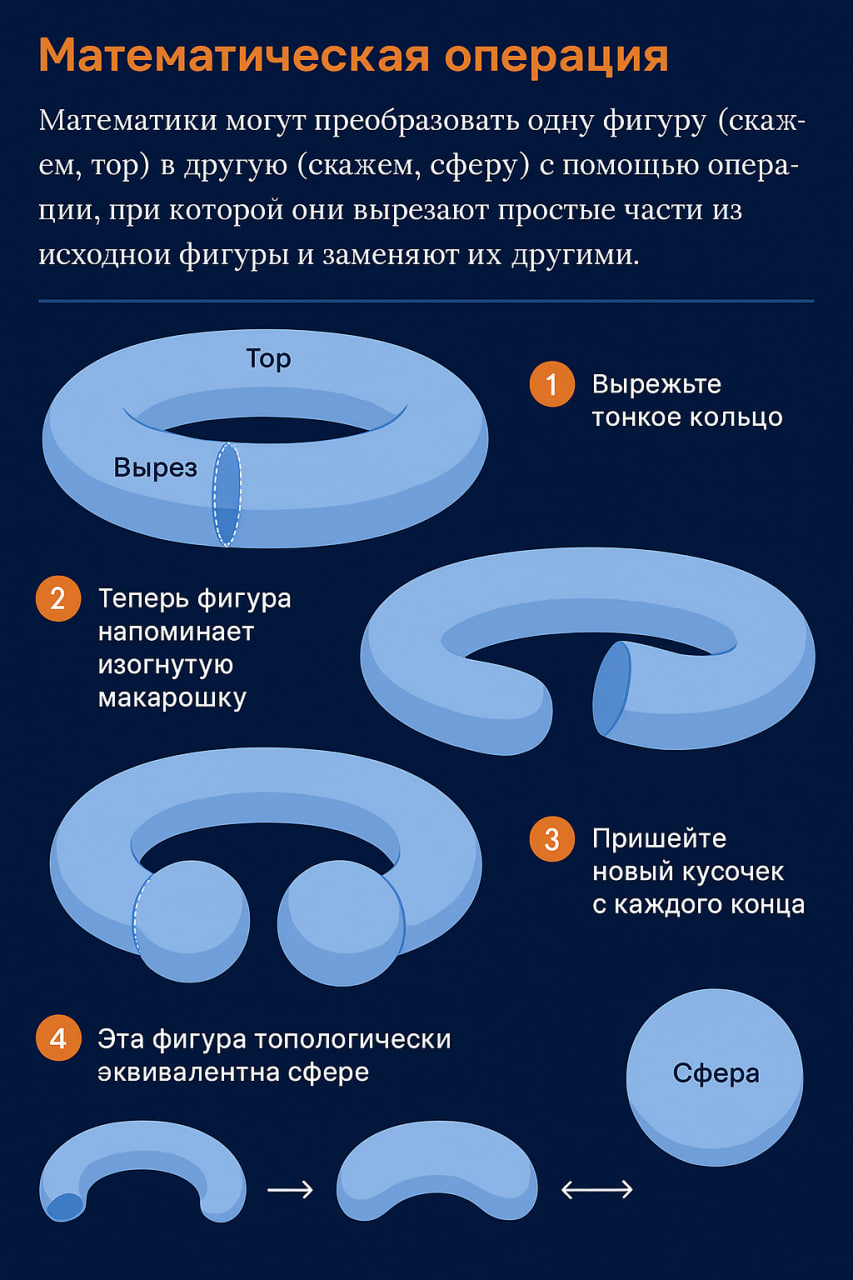
Также важнейший прорыв совершил французский математик Мишель Кервэр в 1960 году, предложив особый параметр - число, вычисляемое для каждого гладкого многообразия. Этот индикатор принимает нулевое значение, если структуру возможно хирургически превратить в сферу, и единичное - если такая трансформация недостижима. Простейший пример: обычный тор характеризуется нулевым показателем Кервэра, тогда как закрученный аналог имеет единичное значение.

Применив свой инструмент к анализу различных измерений, ученый сделал следующее открытие: в десятимерном пространстве существует многообразие, для которого невозможно определить значение инварианта - ни ноль, ни единица не подходят. Это означало обнаружение настолько искривленной конструкции, что само понятие гладкости для нее теряло смысл.

Столь неожиданный результат вызвал всплеск исследовательской активности. Математики начали систематическое изучение инварианта в различных измерениях. Вскоре они доказали существование закрученных структур с единичным показателем в пространствах 2-го, 6-го, 14-го и 30-го рангов. В этих числах прослеживалась закономерность: каждое на два меньше степени двойки. Эта последовательность получила теоретическое обоснование в 1969 году, когда Уильям Браудер математически доказал : единичное значение инварианта возможно только в измерениях такой формы.

Логика подсказывала, что подобные структуры должны существовать во всех пространствах этой последовательности: шестьдесят втором, сто двадцать шестом, двести пятьдесят четвертом. Один из теоретиков даже разработал целую систему гипотез об экзотических конструкциях. Однако вероятность ошибочности исходной идеи породила термин "апокалиптическая гипотеза" - её подтверждение означало бы крах всех связанных концепций.

Первый значимый шаг сделали в 1984 году, когда специалисты подтвердили наличие искомых форм в шестьдесят втором измерении. Однако дальнейшие поиски в пространствах высших порядков не принесли результатов. Постепенно интерес научного сообщества к этой проблематике угас.

В 2009 году Виктор Снейт опубликовал фундаментальный труд, анализирующий следствия существования многообразий с единичным инвариантом во всех размерностях списка Браудера. Предисловие содержало пророческое предупреждение: "Возможно, эта работа описывает несуществующие объекты".

Его предчувствие оправдалось с поразительной быстротой. Через несколько недель после выхода книги группа Хопкинса ошеломила математический мир, представив доказательство "апокалиптической гипотезы": формирование структур с единичным показателем Кервэра невозможно в измерениях выше двести пятьдесят четвертого. Среди бесконечного множества потенциальных конфигураций оставалась неразгаданной лишь тайна пространства сто двадцать шестого ранга.

Цифровой прорыв

В 2011 году молодой математик Чжоули Сюй начал обучение в аспирантуре Чикагского университета, планируя заниматься алгоритмическим анализом геометрических структур. Его руководитель, Питер Мэй , предложил исследовать проблему сто двадцать шестого измерения, требовавшую серьезных вычислительных ресурсов. Наставник направил своего подопечного к легендарному эксперту - Марку Маховальду из Северо-Западного университета, чья увлеченность задачей отразилась даже в названии его яхты "Тетаджей" (θⱼ) - по имени ключевого символа теории.

Маховальд, ушедший из жизни в 2013 году, сразу отклонил эту инициативу, охарактеризовав задачу как "дело всей жизни". Он посоветовал молодому коллеге сосредоточиться на изучении схожих явлений в низших размерностях . Однако загадка высшего порядка продолжала притягивать внимание Сюя, став для него источником постоянного научного вдохновения.

Методология решения была известна специалистам: ключ к пониманию экзотических форм скрывался в особых математических конструкциях - стабильных гомотопических группах . Эти абстрактные объекты представляют собой наборы функций, переносящих точки из сфер высшего ранга на поверхности низших порядков.

Чтобы понять суть этих преобразований, представим отображение, переносящее каждую точку с поверхности сорокачетырехмерной сферы на тридцатитрехмерную. Такая операция фактически "сжимает" одиннадцать координат исходного объекта. При выборе произвольной точки на меньшей сфере и поиске всех её прообразов на большей возникает новая геометрическая структура одиннадцатого ранга.

Анализируя различные точки на сфере низшего порядка, теоретики обнаружили: каждая порождает собственное многообразие. Таким образом, единичное отображение создает не отдельную фигуру, а целое семейство геометрических конструкций. Стабильная гомотопическая группа объединяет множество подобных преобразований в единую математическую систему.

Оказывается, для разрешения вопроса об инварианте Кервэра в конкретном измерении необходимо исследовать стабильную гомотопическую группу этого ранга. Однако здесь возникло серьезное препятствие - понимание таких групп остается одной из сложнейших задач в топологии. По словам Дугласа Равенела, её решение вряд ли будет найдено даже к моменту взросления его внучек.

Математическое сообщество выбрало поэтапный путь исследования. С 1958 года информация о структуре этих групп систематизируется в масштабном каталоге, известном как спектральная последовательность Адамса . Этот атлас, всё еще не завершенный, представляет собой многостраничную систему точек, где каждая страница раскрывает новые аспекты изучаемых объектов.

Работа Браудера показала: ответ на вопрос о существовании особых структур в сто двадцать шестом измерении закодирован в определенной точке соответствующей колонки атласа. Её "выживание" до финальной страницы означало бы разделение всех многообразий этого ранга на два равных класса - с нулевым и единичным показателями Кервэра.

Исследование осложнялось наличием ста пяти потенциальных сценариев исчезновения ключевой точки. Чтобы преодолеть эту преграду, Сюй объединил усилия с давним коллегой Гочжэнь Ваном. Разрабатывая инновационные вычислительные методы, они привлекли к работе Вейнаня Линя. Созданная им программа позволила исключить сто один вариант развития событий. Дальнейший год напряженной работы команда посвятила анализу оставшихся случаев, применяя оригинальные математические подходы. Результат превзошел ожидания: особая точка действительно сохраняется до бесконечной страницы атласа, подтверждая существование искомых структур в пространстве высшего порядка.

"До этого момента научное сообщество считало подобные расчеты невыполнимыми", - прокомментировал Хопкинс. "Исследование демонстрирует беспрецедентные возможности современных вычислительных методов. Разработанные подходы открывают перспективы для картографирования новых областей математического атласа".

Парадокс открытия заключается в том, что, доказав существование необычных геометрических форм в пространстве сто двадцать шестого ранга, математики пока не могут представить метод их построения. Конкретные примеры таких структур найдены лишь в первых четырех особых измерениях последовательности Кервэра - втором, шестом, четырнадцатом и тридцатом. Конструкции более высоких порядков остаются неуловимыми, хотя теоретически должны составлять ровно половину всех возможных геометрических объектов в своих пространствах. "Мы доказали их существование, но пока не можем указать ни на один конкретный пример", - отмечает Тильманн.

Разработка способа конструирования нестандартных фигур в пространствах шестьдесят второго и сто двадцать шестого рангов может раскрыть уникальную природу этих шести измерений - объяснить, почему именно они допускают формирование столь сложно организованных объектов. "В истории математики подобные закономерности обычно указывают на существование глубокой и элегантной теории", - размышляет Хопкинс. "Её особенность должна заключаться в избирательности действия - работать только для нескольких случаев, а не бесконечного множества". Новое исследование стимулирует поиск этой фундаментальной закономерности.

Феномен инварианта Кервэра - лишь одно из проявлений размерностных аномалий, которые отражены в спектральной последовательности Адамса. Особые пространства, допускающие существование закрученных структур, соответствуют шести точкам во второй строке математического атласа. В недавней работе Сюй и Роберт Буркланд из Копенгагенского университета обнаружили признаки иного типа нестандартного поведения в третьей строке каталога. Природа геометрических объектов, соответствующих новым особым точкам, пока остается загадкой, но исследователи полны решимости её разгадать.

По мнению Сюя, дальнейшее изучение последующих уровней атласа может принести новые удивительные открытия. "Математический мир таит множество неразгаданных историй, ожидающих своего часа", - подчеркивает учёный, завершая рассказ об одной из самых интригующих глав современной геометрии.