Основы шифрования (часть 2) - Алгоритм RSA

Автор: Malarkey

Во второй части мы рассмотрим популярный алгоритм RSA, где при шифровании используется публичный ключ. Но вначале хочу предупредить вас еще раз. Код, представленный в этой статье, предназначен только для ознакомительных целей. Криптография – весьма обширная и сложная область, и чтобы у вас не было проблем, я не рекомендую шифровать информацию при помощи моей поделки.

Алгоритм RSA

Шифрование с использованием публичного ключа

Шифрование при помощи публичного ключа используется повсеместно. Если вы хотя бы раз оплачивали что-то в интернете, то уже пользовались этим методом (я надеюсь!). Сразу же возникает вопрос о том, как работает эта защита. Если я ввожу номер своей кредитной карты, чтобы что-то купить, почему кроме адресата никто не может подсмотреть эти сведения? Приведу метафору. Чтобы открыть сейф, вам требуется ключ (или молоток, но, к счастью, сейфы и замки защищены от такого рода деятелей). В шифровании с использованием публичного ключа происходит примерно то же самое. Вы показываете замок на всеобщее обозрение, но ключ от этого замка есть только у избранных, а другими методами открыть дверь практически невозможно.

RSA – один из алгоритмов, реализующих вышеуказанную схему. Кроме того, мы можем использовать этот алгоритм для подтверждения подлинности нашей личности. Если вы, используя секретный ключ, отсылаете кому-то зашифрованное сообщение, адресат при помощи публичного ключа может расшифровать ваше послание. Эта технология позволяет подписывать сообщения, и тем самым подтверждается подлинность отправителя.

Демо-программа на базе алгоритма RSA

Я написал небольшую программу с реализацией шифрования по алгоритму RSA. При помощи флагов –t и –m (с указанием любого целого числа на ваш выбор) демонстрируются базовые возможности шифрования сообщения с использованием публичного ключа.

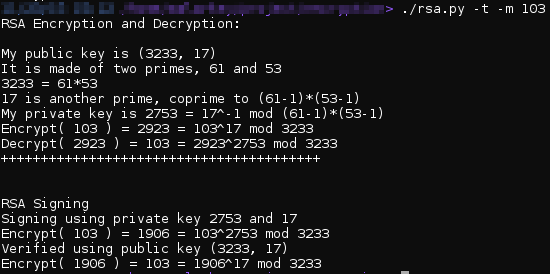
Рисунок 1: Процедура шифрования, дешифрования и цифровой подписи при помощи алгоритма RSA

В примере выше показана пошаговая схема использования публичного и секретного ключа. Публичный ключ состоит из двух чисел: (3233, 17). Первое число (3233) является результатом умножения двух простых чисел (61 и 53). Второе число (17) – простое. Единственный общий множитель двух чисел нашего ключа – единица. Далее мы генерируем секретный ключ, используя выбранные ранее два простых числа. Затем мы можем шифровать и дешифровать сообщения при помощи публичного и секретного ключа соответственно. Если мы хотим подписать сообщение, то используем ключи в обратном порядке (сначала секретный, потом – публичный).

У программы есть дополнительные опции (см. рисунок ниже), позволяющие задавать собственные ключи.

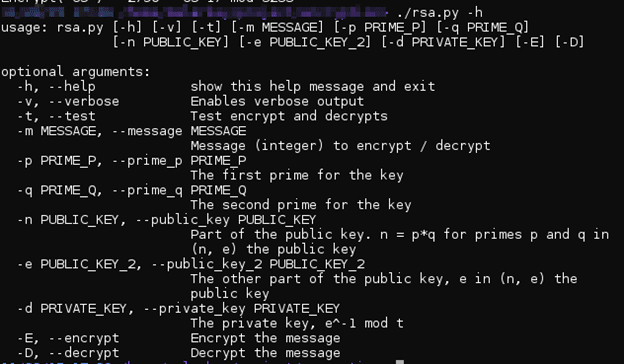
Рисунок 2: Другие опции демонстрационной программы

Один нюанс – программа работает некорректно, если сообщение больше, чем публичный ключ.

Математическая сторона вопроса

RSA во многом схож с алгоритмом Диффи-Хеллмана, поскольку и там и там используется модулярная арифметика. Ниже по шагам рассказывается, как генерируется публичный и секретный ключ.

1. Выбираем два простых числа p и q.
2. Вычисляем n = p*q (часть публичного ключа).
3. Вычисляем тотиент от n, t, который заканчивается числом (p-1)*(q-1).
4. Выбираем простое число e < t и проверяем, чтобы t % e не было равно 0 (e – вторая часть публичного ключа).
5. Вычисляем секретный ключ d = e ^ -1 mod t, где d*e mod t = 1.

Теперь по шагам рассмотрим процесс шифрования и дешифрования:

1. Чтобы зашифровать сообщение, используем формулу E = m^e mod n (m – сообщение).
2. Чтобы расшифровать сообщение, используем формулу E ^ d mod n.

Доказательство того, что Дешифровка( Шифровка ( M ) ) = M приводится в Википедии. Здесь мы еще больше погружаемся в математику и доказательство теорем. Если вы не особо подкованы в этой области, просто попробуйте позапускать скрипт с различными ключами и сообщениями и убедитесь, что все работает корректно.

Рискну предположить, что многим из вас интересно, как взломать систему, построенную на основе алгоритма RSA. Злоумышленник знает числа n и e. Если взломщик сможет найти число t, то вычислит секретный ключ. Задача заключается в том, чтобы факторизовать публичный ключ. Однако целочисленная факторизация – довольно сложная задача, и именно поэтому алгоритм RSA довольно устойчив. Возможно, когда появятся квантовые машины, вычислить секретный ключ не будет составлять особого труда, но сейчас достаточной длинный ключ сможет защитить наши данные.

Дополнительные размышления

При чтении статьи у вас, возможно, возник следующий вопрос: «Как мне удостовериться в том, что полученный публичный ключ именно того человека, которому я хочу отослать сообщение?». Если мы можем обнародовать публичный ключ, то с таким же успехом могли бы поделиться и секретным ключом. Более того, я не могу сходить в офис Амазона и получить от них публичный ключ. Я веду к тому, что мне нужно получить этот ключ каким-то образом. Инфраструктура открытых ключей (Public Key Infrastructure, PKI) – технология, позволяющая управлять всеми этими ключами. Мы используем шифрование для подтверждения наших ключей, предназначенных для шифрования (получается замкнутый круг). Рассмотреть эту проблему в рамках одной статьи не получится. Если вы хотите узнать подробности, гугл вам в помощь.

Кроме того, алгоритм RSA довольно медлителен, и если кому-то удастся вычислить два простых числа, то весь трафик, исходящий от вас, будет расшифрован. В качестве защиты можно предложить следующее. Помните, как я говорил, что тот же самый алгоритм можно использовать для подписи сообщений? Для обмена ключами мы можем использовать алгоритм Диффи-Хеллмана (см. первую часть), а подписывать сообщения при помощи RSA. В итоге наш ключ во время каждой новой сессии будет другим. Используя RSA, мы устанавливаем подлинность адресата. В конечном счете, мы получаем алгоритм для обмена ключами и верификации адресата. Когда-нибудь я напишу программу, реализующую эту технологию.

Надеюсь, вы подчерпнули для себя нечто новое. Шифруйте и подписывайте свои сообщения!

Ссылки

https://en.wikipedia.org/wiki/RSA_(cryptosystem)