Основы шифрования (часть 1) - Алгоритм Диффи-Хеллмана

Автор: Malarkey

Некоторое время назад я проводил исследование, чтобы лучше понять, как устроены криптографические алгоритмы. Сфера применения подобных алгоритмов весьма обширна. Мы защищаем информацию, хранящуюся на дисках или передаваемую через интернет. Мы проводим верификацию отсылаемых сообщений. В некоторых платежных системах шифрование является неотъемлемой частью. Тема криптографии настолько глубока и сложна, что неподготовленному человеку легко запутаться и наделать непоправимых ошибок, и поэтому весь приведенный ниже код не следует использовать в реальных задачах. Основная цель – ознакомиться с базовыми концепциями. Если вы хотите узнать историю вопроса, рекомендую почитать книгу The Code Book. Более детально различные аспекты криптографии описаны в книге Cryptography Engineering. Изучив вышеуказанную литературу, вы сможете лучше понимать, о чем я буду говорить в этой статье.

Суть проблемы

Криптографический ключ необходим для шифрования и дешифрования сообщений. Давайте представим, что мы хотим обмениваться секретными сообщениями через курьера. Если сообщение незашифровано, курьер сможет прочитать его. То есть нам нужно зашифровать переписку, но вначале мы должны передать секретный ключ на другой конец провода. Если мы просто передадим ключ, курьер сможет расшифровать наше послание. Алгоритм Диффи-Хеллмана как раз и призван решить эту задачу.

Алгоритм Диффи-Хеллмана

Рассмотрим схему обмена секретными ключами при помощи алгоритма Диффи-Хеллмана (Diffie-Hellman Key Exchange, DHKE). Более подробно с этой темой можно ознакомиться в русскоязычной и англоязычной Википедии. Ниже показана наглядная схема обмена между двумя пользователями. Алиса и Боб хотят использовать общий ключ для шифрования переписки. Рассмотрим детально этот процесс, используя краски вместо чисел:

1. Алиса и Боб выбрали общую краску.
2. Алиса и Боб выбрали по одной секретной краске.
3. Алиса и Боб смешали общую и секретную краску.
4. Алиса и Боб обменялись получившимися смешанными красками.
5. Алиса смешала полученную смешанную краску от Боба со своей секретной краской.
6. Боб смешал полученную смешанную краску от Алисы со своей секретной краской.
7. Теперь у Алисы и Боба есть общая секретная краска.

(Алиса и Боб будут периодически встречаться в наших рассуждениях, так что привыкайте).

Рисунок 1: Наглядная схема получения общего секретного ключа (из Википедии)

Рабочий пример

Схема обмена секретным ключом реализована мной в коде. Ниже показан результат работы утилиты (для большей наглядности используются дополнительные флаги).

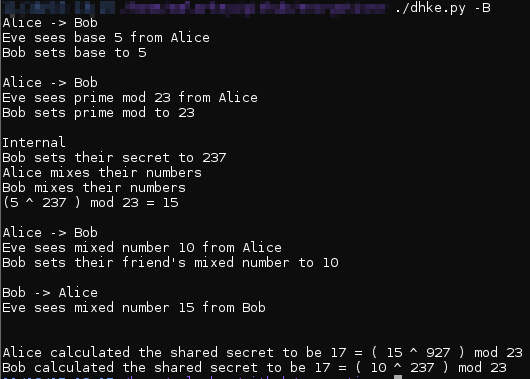
Рисунок 2: Результаты работы скрипта, реализующего алгоритм Диффи-Хеллмана

Небольшие пояснения к Рисунку 2:

• «x -> y» означает, что «x» отсылает сообщение «y»
• «Internal» означает, что действие происходит локально на машине одного из оппонентов

Вначале Алиса выбирает простое базовое число (5) и передает через Еву информацию Бобу. Затем Алиса выбирает еще одно простое число (23), которое будет использоваться при вычислениях, и опять передает через Еву информацию Бобу. Далее Алиса и Боб выбирают секретные числа и производят математические вычисления с использованием чисел 5 и 23. Затем Алиса и Боб через Еву обмениваются полученными сведениями. Далее каждый из оппонентов вычисляет секретный ключ.

Математическая сторона вопроса

«Как же работает этот алгоритм?», - спросите вы. Здесь нам на помощь приходит модулярная арифметика. Рассмотрим выражение g^x mod p. Числа g и p являются эквивалентом общей краски (см. схему выше). Существуют некоторые ограничения относительного того, какие числа можно использовать в качестве g и x (рассмотрим ниже). Число p – простое. Алиса и Боб будут выбирать секретные числа или секретные краски (a и b соответственно). Эти числа могут быть любыми. Затем каждый вычисляет выражение g^x mod p и рассказывает своему оппоненту конечный результат (смешанная краска). Теперь у Алисы есть значение B = g^b mod p, полученное от Боба, а у Боба есть значение A = g^a mod p, полученное от Алисы. Затем оппоненты вычисляют секретный ключ. Алиса вычисляет выражение B^a mod p, а Боб - A^b mod p.

Подождите, B^a mod p и A^b mod p – это и есть секретные ключи? Тогда мы должны быть уверены, что оба выражения дают одинаковый результат. Рассмотрим еще раз весь алгоритм по шагам.

1. Алиса и Боб выбирают два числа g и p.
2. Алиса и Боб выбирают секретные числа (a и b соответственно)
3. Алиса и Боб вычисляют g ^ x mod p, где x – секретное число.
4. Алиса и Боб обмениваются полученными данными (числа A и B соответственно).
5. Алиса и Боб используют полученное число и секретное число для вычисления общего ключа.

В шаге 5 имеем следующее:

У Алисы: B^a mod p = (g^b mod p) ^ a mod p = g^ab mod p.

У Боба: A^b mod p = (g^a mod p) ^ b mod p = g^ab mod p.

Чтобы лучше понять, как работает этот алгоритм, нам придется глубже погрузиться в модулярную арифметику.

Когда вы вычисляете выражение y mod z, на самом деле вычисляется остаток от деления y / z (или y % z, как принято в большинстве языков программирования). Если y < z, тогда y % z = y. Когда y > z выражение работает наподобие часов. По мере увеличения числа y выражение y % z будет равняться значениям в диапазоне от 0 до z – 1. Как только y станет кратно z, отсчет начинается сначала. Выясняется, что операция возведения в степень в модулярной арифметике имеет свойство транзитивности. То есть (a ^ b) ^ c mod d = (a ^ c) ^ b mod d = a^ (b ^ c) mod d. Алиса вычисляет выражение (g^b mod p) ^ a mod p, которое эквивалентно (g^b)^a mod p. В конечном счете, мы получаем выражение g^ab mod p.

Как было сказано ранее, на числа g и p накладываются определенные ограничения. Для выражения a ^ b mod c итоговый результат зависит от выбранных чисел. Рассмотрим выражение: a ^ b mod 7.

2 ^ 1 mod 7 = 2 mod 7 = 2

2 ^ 2 mod 7 = 4 mod 7 = 4

2 ^ 3 mod 7 = 8 mod 7 = 1

2 ^ 4 mod 7 = 16 mod 7 = 2

2 ^ 5 mod 7 = 32 mod 7 = 4

2^ 6 mod 7 = 64 mod 7 = 1

…

Понимаете, в чем дело? В результате мы имеет только 3 различных числа, и количество секретных ключей лишь половина всех чисел, которые меньше 7 (а ограниченное количество ключей напрямую влияет на уровень безопасности).

Вместо 2 возьмем 3:

3 ^ 1 mod 7 = 3 mod 7 = 3

3 ^ 2 mod 7 = 9 mod 7 = 2

3 ^ 3 mod 7 = 27 mod 7 = 6

3 ^ 4 mod 7 = 81 mod 7 = 4

3 ^ 5 mod 7 = 243 mod 7 = 5

3^ 6 mod 7 = 729 mod 7 = 1

….

В этом случае количество возможных секретных ключей возрастает. Если вы хотите глубже ознакомиться с данной темой, рекомендую прочитать эту статью.

Преимущества алгоритма

Алисе и Бобу удалось сгенерировать одинаковый ключ, но насколько решена наша проблема? Рассмотрим ситуацию с позиции Евы (курьера, который передает информацию).

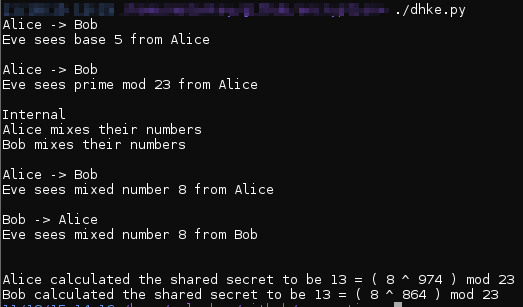
Рисунок 3: Информация, которую видит курьер

Если скрипт запущен без флагов, на выходе показывается информацию, которую видит Ева. В примере выше Ева видит числа g и p, а также A и B. Чтобы вычислить секретный ключ, Еве нужно определить значения числа a (или b), используя выражение A = g^a mod p. Найти решение этого уравнения, которое часто называют секретно вычисляемой функцией (trap door function), довольно сложно. Подобные выражения легко вычисляются в одну сторону, но тяжело в другую (через некоторые двери вы не можете вернуться обратно). Если хотите копнуть глубже, ознакомьтесь со статьей, где описана проблема дискретного логарифмирования.

В итоге Алиса и Боб обменялись секретным ключом и могут пересылать друг другу зашифрованные сообщения. Чтобы еще больше усилить безопасность, мы можем генерировать новые ключи для каждого сеанса связи, и даже если ключ будет вычислен, пострадает только одна сессия.

Во второй части мы рассмотрим алгоритм RSA.

Ссылки

https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange

https://en.wikipedia.org/wiki/Discrete_logarithm_problem

https://en.wikipedia.org/wiki/Primitive_root_modulo_n