Спускаем MAYHEM на двоичный код(часть 2)
В данном документе мы представляем MAYHEM, новую систему для автоматического поиска эксплуатируемых багов в двоичных файлах программ.
Авторы: Sang Kil Cha, Thanassis Avgerinos, Alexandre Rebert и David Brumley
IV. Гибридное символическое выполнение
MAYHEM – система гибридного символического выполнения. Вместо чисто онлайнового или оффлайнового режимов запуска, MAYHEM может преключаться между этими режимами. В данном разделе мы представляем мотивацию и механику гибридного выполнения.
A. Предшествующие системы символического выполнения
Оффлайновое символическое выполнение, имеющее место в системах вроде SAGE [13], требует две порции входных данных – целевой программы и исходного зерна ее аргументов. На первом шаге оффлайновые системы непосредственно запускают программу на зерне и записывают трассировку. На втором шаге они символически запускают инструкции в записанной трассировке. Данный подход называется консимволическим (consolic) выполнением, то есть соединением непосредственного (console) и символического (symbolic) выполнения. Оффлайновое выполнение привлекательно из-за его простоты и низких требований к ресурсам. Нам нужно обрабатывать лишь один путь выполнения за раз.


Рисунок 3: гибридное выполнение пытается сочетать скорость онлайнового выполнения и экономию памяти оффлайнового выполнения для эффективного исследования пространства входных данных.
Левая верхняя диаграмма на рисунке 3 подчеркивает непосредственный недостаток данного подхода. Для каждого исследованного пути выполнения мы сперва должны (потенциально) повторно выполнить очень большое число инструкций, пока не достигнем символического условия разветвеления выполнения и начнем исследовать новые инструкции.
Онлайновое символическое выполнение избегает этих издержек повторного выполнения путем раздвоения интерпретатора в точках ветвления, причем каждый из полученных интерпретаторов имеет копию текущего состояния выполнения. Таким образом, чтобы исследовать новый путь, онлайновое выполнения просто нуждается в выполнении переключения контекста на состояние выполнения приостановленного интерпретатора. S2E [28], KLEE [9] и AEG [2] следуют данным путем, производя онлайновое символическое выполнение LLVM-байткода.
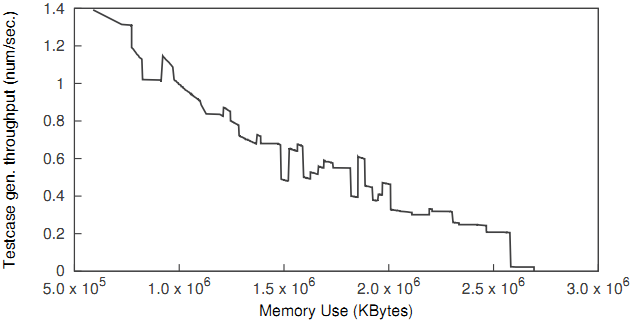

Рисунок 4: Зависимость пропускной способности онлайнового выполнения от использования памяти.
Однако, создание копии выполнителя в каждой точке ветвления программы может быстро истощить память, что приведет к тому, что вся система зависнет. Выдающиеся онлайновые выполнители пытаются решить данную проблему путем агрессивных оптимизаций копирования при записи. Например, KLEE обладает неизменным представлением состояния, а S2E разделяет общее состояние между снимками физической памяти и дисками. Тем не менее, поскольку все состояния выполнения хранятся в памяти одновременно, в итоге все онлайновые выполнители достигнут предела памяти. С данной проблемой можно бороться путем использования поиска в глубину, однако на практике такая стратегия не слишком полезна. Для демонстрации данной проблемы мы скачали S2E [28] и запустили его на приложении echo из coreutils с двумя символическими аргументами по 10 байтов каждый. Рисунок 4 показывает, как пропускная способность символического выполнения (количество тест-кейсов, генерируемых в секунду) снижается при увеличении использования памяти.
B. Гибридное символическое выполнение
MAYHEM вводит гибридное символическое выполнение для активного управления памятью без постоянного повторного выполнения одних и тех же инструкций. Гибридное символическое выполнение переключается между онлайновым и оффлайновым режимами, чтобы максимизировать эффективность каждого из них. MAYHEM начинает анализ в онлайн режиме. Когда система достигает предела памяти, она переключается в оффлайновый режим и перестает размножать выполнители. Вместо этого она создает контрольные точки, чтобы позднее запустить из них новые онлайновые выполнители. Основной проблемой системы является распределение задач онлайнового выполнения между подзадачами без потери потенциально интересующих путей. Алгоритм гибридного выполнения, используемый MAYHEM, делится на четыре основные фазы:
- Инициализация: первый раз, когда MAYHEM вызывается для какой-нибудь программы, он инициализирует менеджер контрольных точек, базу данных контрольных точек и директории тест-кейсов. Затем он начинает онлайновое выполнение программы и переходит к следующей фазе.
- Онлайновое исследование: в ходе онлайновой фазы MAYHEM символически выполняет программу в онлайн-режиме, переключаясь между текущими активными состояниями выполнения и генерируя тест-кейсы.
- Создание контрольных точек: менеджер контрльных точек отслеживает онлайновое выполнение. Всякий раз, когда использование памяти достигает предела или количество запущенных выполнителей превышает заданный порог, он выбирает и генерирует контрольную точку для активного выполнителя. Контрольная точка содержит состояние символического выполнения приостановленного выполнителя (предикаты путей, статистику и т. д.) и информацию для воспроизведения2. Состояние непосредственного выполнения отбрасывается. Когда онлайновое выполнение завершит все активные пути выполнения, MAYHEM переходит к следующей фазе.
- Восстановление контрольных точек: Менеджер контрольных точек выбирает контрольную точку на основе ранжирующей эвристики (§IV-D) и восстанавливает ее в памяти. Поскольку состояние символического выполнения было сохранено в контрольной точке, MAYHEM нужно лишь восстановить состояние непосредственного выполнения. Для этого MAYHEM непосредственно выполняет программу, используя одно из подходящих для выполнения предиката пути значений входных данных, пока программа не достигнет инструкции, в которой было приостановлено состояние выполнения. В данной точке непосредственное состояние восстанавливается и оналайновое исследование (фаза 2) перезапускается. Заметьте, что фаза 4 избегает повторного символического выполнения инструкций в ходе восстановления контрольной точки (в отличие от стандартного консимволического выполнения), и повторное перевыполнение производится лишь непосредственно. Рисунок 3 показывает принцип гибридного выполнения. Мы представим подробное сравнение онлайнового, оффлайнового и гибридного выполнений в §VIII-C.
C. Строение и реализация CEC
CEC принимает на вход двоичную программу, список источников входных данных, которые нужно рассмотреть символически, и (опционально) контрольную точку, которая содержит информацию о состоянии выполнения из предыдущего запуска. CEC выполняет программу непосредственно, перехватывает информацию от источников входных данных и производит taint-анализ входных переменных. Каждый базовый блок, который содержит тентированные инструкции, посылается SES для символического выполнения. В качестве ответа CEC получает адрес следующего базового блока, который нужно выполнить и признак необходимости сохранения текущего состояния в качестве точки восстановления. После завершения пути выполнения CEC переключает контекст на неисследованный путь, выбранный SES, и продолжает выполнение. CEC завершает работу, только если были исследованы все возможные пути выполнения или при достижении порога. Если мы предоставим на вход контрольную точку, CEC сначала непосредственно выполнит программу до данной точки, а затем продолжит выполнение как прежде.
Уровень виртуализации. В ходе онлайнового выполнения CEC обрабатывает множество состояний непосредственного выполнения анализируемой программы одновременно. Каждое состояние непосредственного выполнения содержит текущий контекст регистров, памяти и состояния ОС (состояние ОС включает снимок виртуальной файловой системы, сети и состояния ядра). Под руководством SES и селектора путей CEC переключает контексты между различными состояниями непосредственного выполнения в зависимости от текущего активного символического выполнителя. Уровень виртуализации является посредником всех вызовов к хостовой ОС и эмулирует эти вызовы. Хранение отдельных копий состояния ОС гарантирует, что в ходе разных запусков не будет побочных эффектов. Например, если один выполнитель записывает значение в файл, эта модификация будет видна только для текущего состояния выполнения – все прочие выполнители будут иметь собственные отдельные экземпляры данного файла.
Эффективный снимок состояния. Создание полного снимка состояния непосредственного выполнения для каждой ветви обходится очень дорого. Чтобы бороться с данной проблемой, CEC разделяет состояние между состояниями выполнения – подобно другим системам [9], [28]. Когда выполнение разветвляется, новое состояние выполнения повторно использует состояние родительского выполнения. Последующие модификации состояния записываются в текущем состоянии выполнения.
D. Строение и реализация SES
SES управляет средой символического выполнения и решает, какие пути будет выполнять CEC. Среда символического выполнения состоит из символических выполнителей для каждого пути, селектора путей, который определяет, какой достижимый путь запустить далее, и менеджера контрольных точек.
SES ограничивает число символических выполнителей, удерживающихся в памяти. Когда достигается предел, MAYHEM перестает генерировать новые интерпретаторы и начинает производить контрольные точки – состояния выполнения, соответствующие путям программы, которые MAYHEM не смог исследовать при первом прогоне из-за ограничений памяти. Каждая контрольная точка получает свой приоритет и используется MAYHEM для продолжения исследования соответствующего пути позднее. Таким образом, когда завершаются все рассматриваемые пути выполнения, MAYHEM выбирает новую контрольную точку и продолжает выполнение, пока не будут рассмотрены все контрольные точки.
Каждый символический выполнитель поддерживает два контекста: переменный контекст, содержащий все символические значения регистров и промежуточных данных, и контекст памяти, отслеживающий все символические данные в памяти. Всякий раз, когда выполнение разветвляется, SES клонирует текущее символическое состояние (чтобы использование памяти было низким, мы храним состояние выполнения неизменным для использования оптимизаций копирования при записи, как в предыдущей работе [9], [28]) и добавляет новый символический выполнитель в очередь с приоритетами. Очередь регулярно обновляется нашим селектором пути для включения последних изменений (например, исследованных путей, затронутых инструкций и т. д.).
Предусловное символическое выполнение: MAYHEM реализует предусловное символическое выполнение как AEG [2]. В предусловном символическом выполнении пользователь может опционально задавать частичные спецификации входных данных, вроде префикса или длины, чтобы уменьшить пространство поиска. Если пользователь не предоставляет предусловия, SES пытается исследовать все достижимые пути. Это соответствует пользователю, предоставляющему системе минимальное количество информации.
Выбор пути: MAYHEM применяет для расстановки приоритетов эвристику – как в системах вроде SAGE [13] и KLEE [9] – чтобы решить, какой путь исследовать следующим. На текущий момент MAYHEM использует три правила эвристического ранжирования: а) выполнители, исследующие новый код (вместо очередного запуска уже известного кода), имеют высокий приоритет, б) выполнители, которые определяют символические обращения к памяти, имеют высокий приоритет, в) пути выполнения, где замечены указатели инструкции, имеют высший приоритет. Эвристики разработаны для расстановки приоритетов путей, которые вероятнее всего содержат баги. Например, первая эвристика основана на предположении, что ранее исследованный код содержит баг с меньшей вероятностью, чем новый.
E. Настройка производительности
MAYHEM использует несколько оптимизаций, чтобы ускорить символическое выполнение. Мы представляем наиболее эффективные из них: 1) разбиение на независимые формулы, 2) алгебраическое упрощение и 3) taint-анализ.
Подобно KLEE [9] MAYHEM разбивает предикат пути на независимые формулы для оптимизации запросов к решителю. Небольшое отличие в реализации по сравнению с KLEE состоит в том, что MAYHEM все время поддерживает отображение входных переменных на формулы. Это сделано не только для запросов к решателю (данное представление позволяет дополнительные оптимизации, §V). MAYHEM также применяет другие стандартные оптимизации, предложенные в предшествующих системах вроде оптимизации категоризации ограничений [13], кэш счетчиков [9] и другие. MAYHEM также упрощает символические выражения и формулы путем применения алгебраических упрощений вроде x ⊕ x=0, x & 0 = 0 и т. д.
Возвращаясь к разделу §IV-C, отметим, что MAYHEM использует taint-анализ [11], [23] для выборочного выполнения блоков инструкций, которые работают с символическими данными. Эта оптимизация дает в среднем восьмикратное ускорение по сравнению с выполнением всех блоков инструкций (см. §VIII-G).
V. Индексное моделирование памяти
MAYHEM вводит индексную модель памяти как практический подход для обработки символических обращений к памяти. Индексная модель позволяет MAYHEM адаптировать его интерпретацию символической памяти на основе значения индекса. В данном разделе мы представляем полную модель памяти MAYHEM.
MAYHEM моделирует память как отображение μ: I → E 32-битных индексов (i) на выражения (e). В выражении load(μ,i) мы говорим, что индекс i индексирует память μ, а загруженное значениеe представляет содержимое i-й ячейки памяти. Чтение по конкретному индексу i напрямую транслируется MAYHEM в чтение соответствующей ячейки в μ (т. е., μ[i]). Инструкция store(μ, i, e) приводит к созданию новой памяти μ[i ← e], где i отображается в e.
A. Предшествующие работы и моделирование символических индексов
Символический индекс имеет место, когда индекс, используемый для обращения к памяти, является не числом а выражением — шаблоном, который очень часто встречается в двоичном коде. Например, C-оператор switch(c) компилируется в просмотр таблицы переходов, где введенный символ c используется в качестве индекса. Все стандартные функции преобразования (вроде ASCII в Unicode и обратно) попадают в данную категорию.
Известно, что обработка произвольных символических индексов трудна, поскольку символический индекс может (в худшем случае) ссылаться на любую ячейку памяти. Предыдущие исследования и передовые инструменты показывают, что существует два основных подхода к обработке символических индексов: a) конкретизация индексов и b) полностью символическая память.
Конкретизация означает, что вместо построения заключения о всех возможных значениях, которые могут быть проиндексированы в памяти, мы конкретизируем индекс единственным специфическим адресом. Данная конкретизация может снизить сложность производимых формул и улучшить время решения/исследования. Однако, ограничение индекса одним единственным значением может привести к потере путей выполнения - например, если они зависят от значения индекса. Конкретизация - естественный выбор для оффлайновых выполнителей вроде SAGE [13] или BitBlaze [5], поскольку в ходе непосредственного выполнения обращение происходит только по одному адресу.
Построение заключений о всех возможных индексах также возможно, если рассматривать память как целиком символическую. Например, инструменты вроде McVeto [27], BAP [15] и BitBlaze [5] могут обрабатывать символическую память. Главный недостаток по сравнению с конкретизационным подходом - производительность. Формулы, работающие с символической памятью более обширны и потому время решения/исследования обычно больше.
B. Моделирование памяти в MAYHEM
Первая реализация MAYHEM использовала простой конкретизационный подход и конкретизировала все индексы памяти. Это решение оказалось крайне ограничивающим, поскольку выбор единственного адреса для индекса обычно не позволяет нам выполнить требования к полезной начинке эксплоита. Наши эксперименты показали, что 40% образцов программ требуют обработки символической памяти – простая конкретизация для них оказалась неэффективной (см. §VIII).
Альтернативный подход – символическая память. Для избежания проблем расширяемости, связанных с полностью символической памятью, MAYHEM моделирует память частями, где запись всегда конкретизируется, но символические чтения могут моделироваться символически. В оставшейся части раздела мы подробно опишем индексную модель памяти MAYHEM, равно как и некоторые ключевые оптимизации.
Объекты памяти. Для моделирования символических считываний, MAYHEM вводит понятие объектов памяти. Подобно глобальной памяти μ, объект памяти M также является отображением 32-битных индексов на выражения. Однако, в отличие от глобальной памяти, объект памяти неизменяем. Каждый раз, когда символический индекс используется для чтения памяти, MAYHEM генерирует свежий объект памяти M, содержащий все значения, к которым можно получить доступ по индексу – M является частичным снимком глобальной памяти.
Используя объекты памяти, MAYHEM может сократить вычисление выражения load(μ, i) до M[i]. Отметим, что это семантически эквивалентно возврату μ[i]. Ключевое отличие в размере символического массива, вводимого в формуле. В большинстве случаев объект памяти M будет на порядки меньше, чем полная память μ.
Разрешение границ объектов памяти. Создание объекта памяти требует от MAYHEM нахождения всех возможных значений символического индекса i. В худшем случае это может потребовать 232 запросов к решателю (для 32-битных адресов). Для решения этой проблемы MAYHEM повышает расширяемость за счет некоторого количества точности путем разрешения границ [L, U]региона памяти, где L – нижняя граница индекса, а U – верхняя. Границы должны быть консервативными, т. е. все возможные значения индекса должны лежать между L и U. Отметим, что регион памяти не обязан быть непрерывным, например, он может включать лишь два значения (L и U).
Чтобы получить эти границы, MAYHEM использует решатель для выполнения двоичного поиска значения индекса в контексте текущего предиката пути. Например, изначально для нижней границы 32-битного i: L ∈ [0, 232 - 1]. Если выполнено i < (232 - 1) / 2 , то L ∈ [0, (232 - 1) / 2 - 1], иначе L ∈ [(232 - 1) / 2, 232 - 1]. Мы повторяем данный процесс пока не восстановим обе границы. Используя границы, мы можем теперь создать объект памяти (используя новый символический массив M) следующим образом: ∀i ∈ [L, U]: M[i] = μ[i].
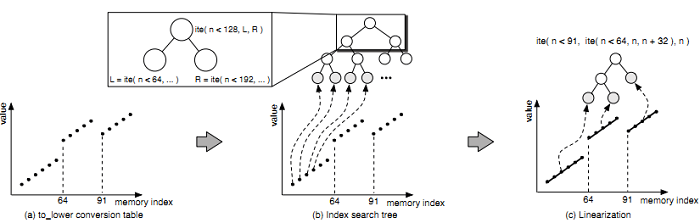

Рисунок 5: (a) - таблица преобразования to_lower, (b) - сгенерированное IST, (c) - IST после линеаризации.
Алгоритм разрешения границ, описанный выше, достаточен для генерации консервативного представления объектов памяти и позволяет MAYHEM делать заключения о символических считываниях памяти. В оставшейся части раздела мы рассмотрим основные методы оптимизации, которые включает MAYHEM для устранения некоторых недостатков исходного алгоритма:
- Запрос к решателю для каждого разыменовывания символической памяти стоит дорого. Даже при двоичном поиске определение обоих границ 32-битного индекса требует в среднем примерно 54 запроса (§VIII) (§V-B1,§V-B2,§V-B3).
- Регион памяти может не быть непрерывным. Даже хотя многие значения между границами могут быть недостижимыми, они все еще включены в объект памяти, а значит и в формулу (§V-B2).
- Значения в объекте памяти могут иметь структуру. Моделируя объект как единый массив байтов мы упускаем возможности оптимизации наших формул на основе структуры (§V-B4,§V-B5).
- В худшем случае символический индекс может обратиться к любому возможному месту в памяти (§V-C).
1) Анализ набора значений (Value Set Analysis, VSA). MAYHEM использует онлайновую версию VSA [4] для сокращения нагрузки на решатель при разрешении границ символического индекса (i). VSA возвращает шаговый интервал для заданного символического индекса. Шаговый интервал представляет собой набор значений в виде S[L, U], где S – шаг, а L и U – границы. Например, интервал 2[1,5] соответствует набору значений {1,3,5}. Возвращаемый VSA шаговый интервал будет аппроксимацией сверху всех возможных значений индекса. Например, результатом для i = (1 + byte) << 1 где byte – символический байт с интервалом 1[0,255], будет VSA(i) = 2[2,512].
Шаговый интервал, производимый VSA, затем уточняется решателем (используя все ту же стратегию двоичного поиска) для получения строгих нижней и верхней границ объекта памяти. Например, если предикат пути утверждает, что byte < 32, тогда интервал для индекса (1 + byte) << 1 может быть уточнен до 2[2,64]. Использование VSA для предобработки имеет каскадный эффект на моделирование памяти: a) мы производим на 70% меньше запросов для разрешения точных границ объекта памяти (§VIII), b) шаговый интервал можно использовать для исключения невозможных значений региона [L, U], что упрощает формулы, c) исключение невозможных значений может привести в действие другие оптимизации (см. §V-B5).
2) Кэш уточнений: каждый интервал VSA уточняется с помощью запросов к решателю. Процесс уточнения все еще может быть дорогим (например, верхняя оценка, возвращаемая VSA, может быть слишком грубой). Чтобы избежать повторения процесса для одних и тех же интервалов, MAYHEM хранит кэш отображений интервалов на потенциальные уточнения. Когда происходит попадание в кэш, мы запрашиваем решатель для проверки того, подходит ли кэшированное уточнение для текущего символического индекса, перед обращением к двоичному поиску. Кэш уточнений может сократить количество запросов на разрешение границ на 82% (§VIII).
3) Кэш лемм: проверка записи в кэше уточнений все еще нуждается в запросах к решателю. MAYHEM использует еще один уровень кэширования для избежания повторных запросов α-эквивалентных формул, т. е. формул, которые структурно эквивалентны до переименования переменных. Для этого MAYHEM преобразует структурно эквивалентные формулы в каноническое представление (F) и кэширует результат запросов (Q) в форму лемм: F → Q. Ответ для любой формулы, отображающейся в то же каноническое представление, немедленно извлекается из кэша. Кэш лемм может снизить количество запросов на разрешение границ до 96% (§VIII). Эффективность данного кэша зависит от оптимизации, связанной с разбиением на независимые формулы (§IV-E). Предикат пути необходимо представить в виде набора независимых формул, иначе добавление любой новой формулы к текущему предикату пути сделает недействительными все прежние записи в кэше лемм.
4) Индексные деревья поиска (IST): Любое значение, загруженное из объекта памяти M, является символическим. Чтобы разрешить ограничения, касающиеся загруженного значения (M[i]), решателю нужно найти запись в объекте, которая удовлетворяет ограничениям, и убедиться, что ее индекс является корректным. Для облегчения нагрузки на решатель MAYHEM замещает выражения поиска объектов памяти индексными деревьями поиска (IST). IST – двоичное дерево поиска, в котором ключом является символический индекс, а листья содержат записи объекта. IST целиком закодировано в прдеставлении формулы выражения загрузки значения из памяти.
Более точно, при заданном (отсортированном по адресу) списке записей E объекта памяти M сбалансированное IST для символического индекса i определяется как: IST(E)= ite(i < addr(Eright),Eleft, Eright), где ite представляет условное выражение if-then-else, Eleft (Eright) – левую (правую) половину исходных записей E, а addr(.) возвращает наименьший адрес заданных элементов. Для единственной записи IST возвращает эту запись без построения ite-выражений.
Отметим, что вышеприведенное определение строит сбалансированное IST. Вместо этого мы можем построить IST с вложенными ite-выражениями, при этом глубину формулы можно оценить O(n), где n – количество записей объекта, вместо O(log n). Однако, наши экспериментальные результаты показывают, что сбалансированное IST в 4 раза быстрее, чем вложенное IST (§VIII). Рисунок 5 показывает, как MAYHEM строит IST по заданным записям объекта памяти (таблица преобразования to_lower) с единственным символическим символом в качестве индекса.
5) Сегментация линейными функциями: алгоритм генерации IST создает листовой узел для каждой записи объекта памяти. Для уменьшения числа записей, MAYHEM делает дополнительный шаг предобработки перед передачей объекта в IST. Идея в том, что мы можем использовать структуру объекта памяти для комбинации множества записей в одном сегменте. Сегмент – это параметризованное индексом выражение, которое возвращает значение объекта памяти для каждого индекса из диапазона.
Для генерации сегментов MAYHEM использует линейные функции. А именно, MAYHEM развертывает все записи объекта памяти и соединяет последовательные точки (пары <индекс, значение>) в линии в ходе процесса, который мы называем линеаризацией. Любые две точки могут формировать линию y = αx + β. Последующие точки (ii, vi) будут находиться на той же линии, если vi = αii + β. В конце линеаризации объект памяти разбивается на список сегментов, каждый из которых является линией или изолированной точкой. Данный список сегментов теперь может быть передан в алгоритм IST. Рисунок 5 показывает to_lower IST после применения линеаризации. Линеаризация эффективно уменьшает количество листовых узлов с 256 до 3.
Идея использования линейных функций для упрощения поиска в памяти исходит из простого наблюдения: на двоичном уровне для некоторых операций часто появляются шаблоны линейного вида. Например, таблицы переходов, генерируемые переключателями (switch), таблицы конвертации и трансляции (ASCII в Unicode и обратно) – все они содержат значения, которые растут линейно вместе с индексом.
C. Конкретизация с приоритетами.
Моделирование символических загрузок из памяти с помощью объектов памяти выгодно, когда размер этих объектов значительно меньше объема всей памяти (|M| << |μ|). Таким образом, оптимизации вступают в действие только, когда объект памяти, аппроксимированный диапазоном, меньше порогового значения (в наших экспериментах оно равно 1024).
Всякий раз, когда размер объекта памяти превышает порог, MAYHEM конкретизирует индекс, используемый для обращения к объекту. Однако, вместо выбора подходящего значения случайным образом, MAYHEM пытается приоритезировать возможные конкретные значения. Для каждого символического указателя MAYHEM производит три проверки:
- Проверка, что можно перенаправить указатель на неотображенную часть памяти в контексте текущего предиката пути. Если можно, MAYHEM генерирует тест-кейс аварийного завершения для подходящего значения.
- Проверка, что можно перенаправить символический указатель на символические данные. Если да, то MAYHEM перенаправляет (и конкретизирует) указатель на наименее ограниченный регион символических данных. Путем перенаправления указателя на наименее ограниченный регион, MAYHEM пытается избежать загрузки чересчур ограниченных значений, исключая, таким образом, потенциальные пути, зависящие от этих значений. Для определения наименее ограниченного региона, MAYHEM делит память на символические регионы и сортирует их на основе сложности связанных с ними ограничений.
- Если все ранее указанные проверки неудачны, MAYHEM конкретизирует индекс к корректному адресу памяти и продолжает выполнение.
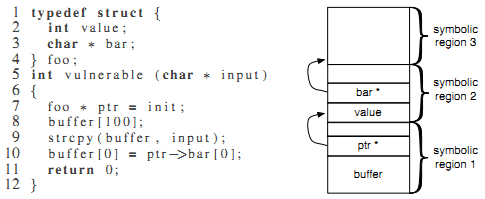

Рисунок 6: MAYHEM восстанавливает структуры символических данных.
Данные шаги позволяют определить, является ли символическое выражение указателем и, если да, то определить, корректен ли он или нет (скажем, NULL-указатель). Например, на рисунке 6 видно переполнение буфера в строке 9. Однако, атакующий не обязательно перехватит управление, даже если strcpy перезапишет адрес возврата. Для передачи управления данной программе нужно достичь инструкции возврата. В строке 10 программа производит два разыменовывания, каждое из которых должно быть успешным (не привести к аварийному завершению) для достижения строки 11 (отметим, что указатель ptr уже перезаписан пользовательскими данными). MAYHEM с включенной приоритезированной конкретизацией сгенерирует три тест-кейса: 1) аварийный тест-кейс для некорректного разыменовывания указателя ptr, 2) аварийный тест-кейс для случая, когда не удается разыменовать указатель после успешного перенаправления ptr на символические данные, и 3) тест-кейс эксплоита, в ходе которого оба разыменовывания успешны и пользовательские данные перехватывают управление программой. Рисунок 6 показывает разметку памяти для третьего случая.
VI. Генерация эксплоитов
MAYHEM проверяет два эксплуатируемых свойства: символический (тентированный) указатель на инструкцию и символическую строку формата. Эти свойства соответствуют переполнению буфера и атаке на строку формата. Если одна из эксплуатируемых политик нарушается, MAYHEM генерирует формулу эксплуатируемости и пытается найти подходящий ответ, то есть эксплоит.
MAYHEM может генерировать как локальные, так и удаленные атаки. Строение MAYHEM позволяет обрабатывать оба этих типа атак схожим образом. Для Windows-программ MAYHEM обнаруживает перезаписанные структурированные обработчики исключений (SEH) в стеке при возникновении исключительных ситуаций и пытается создать основанный на SEH эксплоит.
Переполнения буфера: MAYHEM генерирует эксплоиты для любой возможной перезаписи указателя инструкции, обычно совершаемой при переполнении буфера. Когда MAYHEM находит символический указатель на инструкцию, он сначала пытается сгенерировать эксплоиты типа jump-to-register, как в предыдущей работе [14]. Для этого типа эксплоитов указатель на инструкцию должен указывать на «трамплин», например, jmp %eax, а регистр, например, %eax, должен указывать на место в памяти, в котором мы можем поместить наш шеллкод. Закодировав данные ограничения в формуле, MAYHEM может запросить у решателя приемлемый ответ. Если ответ существует, значит мы доказали, что баг эксплуатируем. Если мы не можем сгенерировать эксплоит типа jump-to-register, мы пробуем сгенерировать более простой эксплоит, направляющий указатель инструкции в то место, где мы можем поместить шеллкод.
Атаки на строки формата: для обнаружения и генерирования атак на строки формата MAYHEM проверяет, содержат ли аргументы формата функций вроде printf символические байты. Если символические байты обнаружены, он пытается поместить полезную нагрузку строки формата в аргумент, который перезапишет адрес возврата форматирующей функции.
Примечания
1 Здесь используется менее формальный, но более емкий термин "баг" вместо "программная ошибка"
2 Заметим, что термин "контрольная точка" отличается от "зерна" оффлайнового выполнения, которое является лишь конкретными входными данными.
Ссылки
[1] "Orzhttpd, a small and high performance http server," http://code.google.com/p/orzhttpd/.
[2] T. Avgerinos, S. K. Cha, B. L. T. Hao, and D. Brumley, "AEG: Automatic exploit generation," in Proc. of the Network and Distributed System Security Symposium, Feb. 2011.
[3] D. Babi´ c, L. Martignoni, S. McCamant, and D. Song, "Statically-Directed Dynamic Automated Test Generation," in International Symposium on Software Testing and Analysis. New York, NY, USA: ACM Press, 2011, pp. 12–22.
[4] G. Balakrishnan and T. Reps, "Analyzing memory accesses in x86 executables." in Proc. of the International Conference on Compiler Construction, 2004.
[5] "BitBlaze binary analysis project," http://bitblaze.cs.berkeley.edu, 2007.
[6] BitTurner, "BitTurner," http://www.bitturner.com.
[7] D. Brumley, P. Poosankam, D. Song, and J. Zheng, "Automatic patch-based exploit generation is possible: Techniques and implications," in Proc. of the IEEE Symposium on Security and Privacy, May 2008.
[8] J. Caballero, P. Poosankam, S. McCamant, D. Babic, and D. Song, "Input generation via decomposition and re-stitching: Finding bugs in malware," in Proc. of the ACM Conference on Computer and Communications Security, Chicago, IL, October 2010.
[9] C. Cadar, D. Dunbar, and D. Engler, "KLEE: Unassisted and automatic generation of high-coverage tests for complex systems programs," in Proc. of the USENIX Symposium on Operating System Design and Implementation, Dec. 2008.
[10] M. Costa, M. Castro, L. Zhou, L. Zhang, and M. Peinado, "Bouncer: Securing software by blocking bad input," in Symposium on Operating Systems Principles, Oct. 2007.
[11] J. R. Crandall and F. Chong, "Minos: Architectural support for software security through control data integrity," in Proc. of the International Symposium on Microarchitecture, Dec. 2004.
[12] L. M. de Moura and N. Bjørner, "Z3: An efficient smt solver," in TACAS, 2008, pp. 337–340.
[13] P. Godefroid, M. Levin, and D. Molnar, "Automated whitebox fuzz testing," in Proc. of the Network and Distributed System Security Symposium, Feb. 2008.
[14] S. Heelan, "Automatic Generation of Control Flow Hijacking Exploits for Software Vulnerabilities," Oxford University, Tech. Rep. MSc Thesis, 2002.
[15] I. Jager, T. Avgerinos, E. J. Schwartz, and D. Brumley, "BAP: A binary analysis platform," in Proc. of the Conference on Computer Aided Verification, 2011.
[16] J. King, "Symbolic execution and program testing," Commu- nications of the ACM, vol. 19, pp. 386–394, 1976.
[17] Launchpad, https://bugs.launchpad.net/ubuntu, open bugs in Ubuntu. Checked 03/04/12.
[18] C.-K. Luk, R. Cohn, R. Muth, H. Patil, A. Klauser, G. Lowney, S. Wallace, V. J. Reddi, and K. Hazelwood, "Pin: Building customized program analysis tools with dynamic instrumentation," in Proc. of the ACM Conference on Programming Language Design and Implementation, Jun. 2005.
[19] R. Majumdar and K. Sen, "Hybrid concolic testing," in Proc. of the ACM Conference on Software Engineering, 2007, pp. 416–426.
[20] L. Martignoni, S. McCamant, P. Poosankam, D. Song, and P. Maniatis, "Path-exploration lifting: Hi-fi tests for lo-fi emulators," in Proc. of the International Conference on Architectural Support for Programming Languages and Operating Systems, London, UK, Mar. 2012.
[21] A. Moser, C. Kruegel, and E. Kirda, "Exploring multiple execution paths for malware analysis," in Proc. of the IEEE Symposium on Security and Privacy, 2007.
[22] T. Newsham, "Format string attacks," Guardent, Inc., Tech. Rep., 2000.
[23] J. Newsome and D. Song, "Dynamic taint analysis for automatic detection, analysis, and signature generation of exploits on commodity software," in Proc. of the Network and Distributed System Security Symposium, Feb. 2005.
[24] E. J. Schwartz, T. Avgerinos, and D. Brumley, "All you ever wanted to know about dynamic taint analysis and forward symbolic execution (but might have been afraid to ask)," in Proc. of the IEEE Symposium on Security and Privacy, May 2010, pp. 317–331.
[25] E. J. Schwartz, T. Avgerinos, and D. Brumley, "Q: Exploit hardening made easy," in Proc. of the USENIX Security Symposium, 2011.
[26] K. Sen, D. Marinov, and G. Agha, "CUTE: A concolic unit testing engine for C," in Proc. of the ACM Symposium on the Foundations of Software Engineering, 2005.
[27] A. V. Thakur, J. Lim, A. Lal, A. Burton, E. Driscoll, M. Elder, T. Andersen, and T. W. Reps, "Directed proof generation for machine code," in CAV, 2010, pp. 288–305.
[28] G. C. Vitaly Chipounov, Volodymyr Kuznetsov, "S2E: A platform for in-vivo multi-path analysis of software systems," in Proc. of the International Conference on Architectural Support for Programming Languages and Operating Systems, 2011, pp. 265–278.
Цифровые следы - ваша слабость, и хакеры это знают.
